前回のレッスンでシャープ、フラットの付いた音符を含む音程を学びました。
今回は複音程と転回音程を解説します。
この2つをもって覚えるべき音程の種類は全て完了となります!
複音程
複音程とは完全8度を超える音程を指します。
増8度も複音程に含まれるので注意しましょう。
※完全8度以内の音程は単音程と言います。

複音程の数え方
複音程の数え方は単音程と変わりません。
下の音符から順番に1度、2度…と数えて9度、10度となります。

もしくは、1オクターブと2度や、1オクターブと6度といった数え方もします。

こちらの数え方は下の音符を1オクターブや2オクターブと上げていき、上の音と下の音が1オクターブ以内の音程になるようにします。

そこからは今まで通り、単音程のときと同じ数え方をすれば「○オクターブと○度」と数えることができます。
複音程の長、短、完全などの付き方
こちらも単音程のときとかわらず、長9度や完全12度などと呼びます。
長、短、完全の付け方は「1オクターブと2度」といった下の音と上の音が1オクターブ以内になるように調整した状態にし、単音程のときと同じように数えます。
実際の例を見てみましょう。
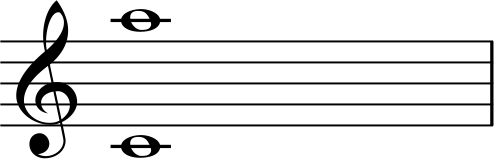
下の音がド、上の音がラです。
音程が1オクターブ以内になるように下の音を1オクターブ上げます。

これで単音程として数えることができるようになりました。
この音程は最初に1オクターブ分、下の音を上げたので、
「1オクターブと長6度」
となります。
もう一つ例を見てみましょう。
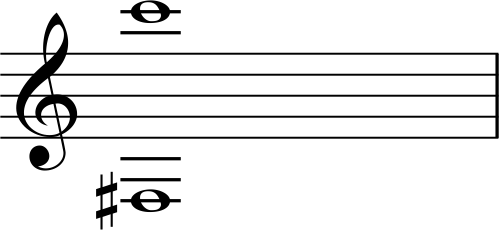
下の音はファのシャープ、上の音はドです。
音程を1オクターブ以内にするには下の音をまず2オクターブあげます。
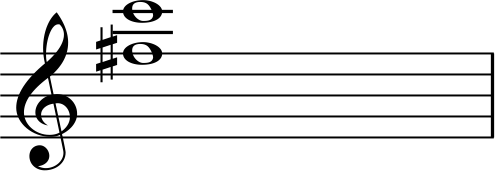
これで単音程として読めるようになりました。
変化記号や調号が付いていても(シャープやフラットがついていても)読み方は単音程のときと何もかわりません。
なのでこの音程は
「2オクターブと減5度」
となります。
転回音程
転回音程とは上下の音を逆にしてできる音程です。
例えばドとミの転回音程はミとド、レとソの転回音程はソとレなどです。
※ただし、複音程には転回音程が存在しません。

度数の転回は?
転回音程にはある一定の法則があります。
元の音程が3度の場合、転回音程は6度になります。

元の音程が4度の場合、転回音程は5度になります。

長、短、完全の転回は?
では長、短、完全などはどうなるのでしょうか?
まずは前回のレッスンで覚えた音程変化の図を思い出してください。
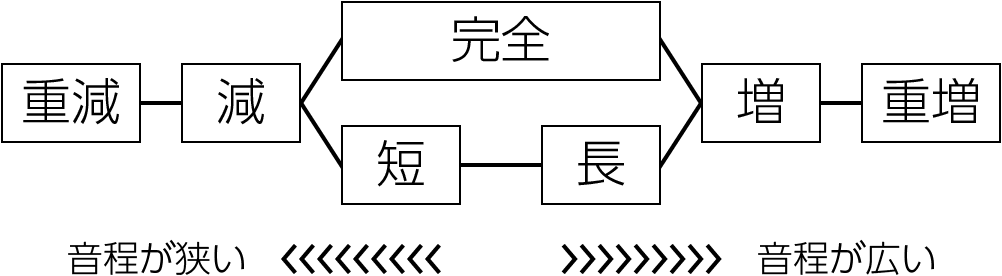
転回音程の長短完全の付き方にも、度数と同じように法則があります。
ただし、完全○度は転回音程になっても完全○度のままです。
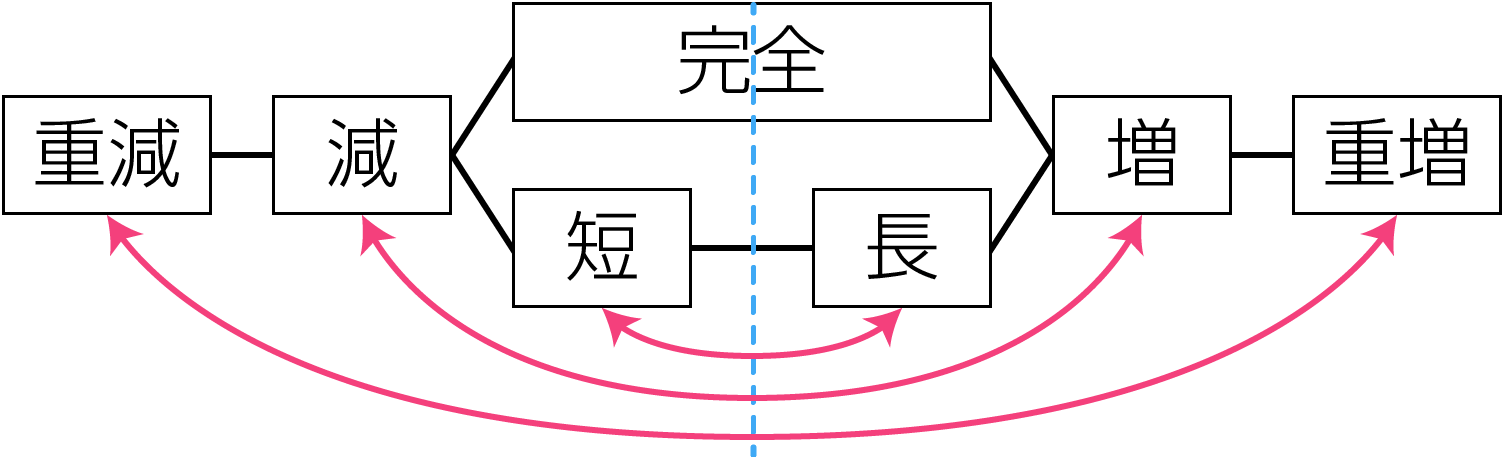
例えば、このようになります。
- 長○度の転回音程は短○度
- 減○度の転回音程は増○度
- 重増○度の転回音程は重減○度
- 完全○度の転回音程は完全○度
転回音程の実例
度数、長短などをあわせて転回音程を作ってみましょう。
※説明のために楽譜を書いていますが、上2つの法則を使えば楽譜なしでも転回音程は求めれます。
ドとミは長3度です。
転回音程のミとドは短6度です。

ファとドは完全5度です。
転回音程のドとファは完全4度です。

シとファは減5度です。
転回音程のファとシは増4度です。

ソbとレ#は重増5度です。
転回音程のレ#とソbは重減4度です。

まとめ
さて、これにて音楽理論の基礎である「音程」の解説はすべて完了しました。
はじめて音程について勉強された方には少々難しかったのではないでしょうか?
音程が難しいとされる理由にはいくつかあります。
- 覚えることが多い
- シャープやフラットが付くと分からなくなる
- 分かるけど答えを出すまでに時間がかかる
おおよそ、このような点でつまずきがちです。
実際に音程は覚えることが多いです。しかし、1つ1つ闇雲に覚えるのではなく、それぞれの音程の関係性を理解した上で覚えることで、より強固な記憶として定着していきます。
シャープやフラットが付くと分からなくなる、また、分かるけど答えを出すまでに時間がかかるといった場合には、音程の記事を最初から読み進めることをおすすめします。
人間の記憶は思いの外、曖昧ですが、だれでも回数を重ねて読むことで必ず理解が深まっていきます。
仕組みで覚えるスケールへ進む
1. スケールの読み方、種類と音度